Trong toán học có khá nhiều câu chuyện lý
thú, có nhiều lĩnh vực toán học được hình thành từ những sự việc rất tình cờ.
Graph toán học hay lý thuyết đồ thị là một trong những lĩnh vực được hình thành
theo cách như vậy.
Câu chuyện về 7 cây cầu ở Königsberg.
Vào thế kỷ thứ 18, tại một thành phố
cổ của nước Nga có 7 cây cầu được xây dựng để nối liền các bờ sông hoặc các
vùng đất của thành phố lại với nhau như hình bên dưới đây.
Khi đi du lịch ở thành phố này mọi người phát hiện ra một vấn đề là “muốn đi qua tất cả các cây cầu của thành phố thì ít nhất phải đi qua 1 cây cầu nào đó hai lần”.
Người dân ở Königsberg đã đặt ra một
câu đố và chưa có ai giải được đó là: "Liệu có thể đi một lần
qua tất cả 7 chiếc cầu mà không phải lặp lại hay không (mỗi cây cầu chỉ được đi
qua một lần duy nhất) không kể điểm xuất phát hay kết thúc ở đâu?".
Câu đố thú vị này đã khiến rất nhiều
người tới nơi đây và “đi dạo” thử để giải nó! Thế nhưng kết quả là tất cả đều
thất bại và không ai tìm ra được phương án nào thoả mãn bài toán.
Cho mãi tới năm 1735, một nhà toán học
lỗi lạc đã tình cờ nghe được câu chuyện này và bắt tay vào nghiên cứu nó. Người
đó chính là thiên tài người Thụy Sĩ - Leonhard Euler (1707 - 1783). Sau
khi nghiên cứu thì Euler đã chứng minh được rằng bài toán này không có lời giải
hay không thể thực hiện được yêu cầu trên và việc làm của nhiều
người là vô ích khi đâm đầu tìm kiếm một phương án khả thi.
Euler đã giải bài toán này như thế nào?
Thoạt nhìn thì đây có vẻ là một câu đố
bình thường, thế nhưng nó lại ẩn chứa mối liên hệ sâu sắc giữa lý thuyết đồ thị
và Tôpô học sau này, chính việc giải bài toán này đã giúp Euler mở ra một nhánh
mới trong toán học đó là “Lý thuyết đồ thị” hay Graph Toán học!
Graph là gì?
Một Graph được định nghĩa là một tập hợp gồm hữu hạn các điểm (gọi là các đỉnh của Graph) và hữu hạn các đoạn thẳng hoặc cong (gọi là các cạnh của Graph) có các đầu mút là các đỉnh của Graph.
Các đỉnh của Graph sẽ được ký hiệu bằng các chữ cái A, B, C, D, ...
Cạnh được nối bởi hai đỉnh A và B được gọi là cạnh AB hoặc cạnh BA.
Hiển nhiên là một đỉnh có thể là đầu mút cho nhiều cạnh hoặc không có cạnh nào.
Một đỉnh của Graph được gọi là đỉnh bậc n nếu nó là đầu mút của n cạnh.
Nếu một đỉnh không là đầu mút của cạnh nào thì ta gọi là đỉnh cô lập.
Một cạnh của Graph sẽ có đầu mút là 2 đỉnh khác nhau hoặc có đầu mút là một đỉnh duy nhất.
Nếu một cạnh có hai đầu mút trùng nhau thì ta gọi là một khuyên.
Hai đỉnh có ít nhất 1 cạnh nối giữa chúng được gọi là hai đỉnh kề nhau.
Hai cạnh có chung một đầu mút là hai cạnh liên tiếp.
Ví dụ:
Ta có hình vẽ sau đây.
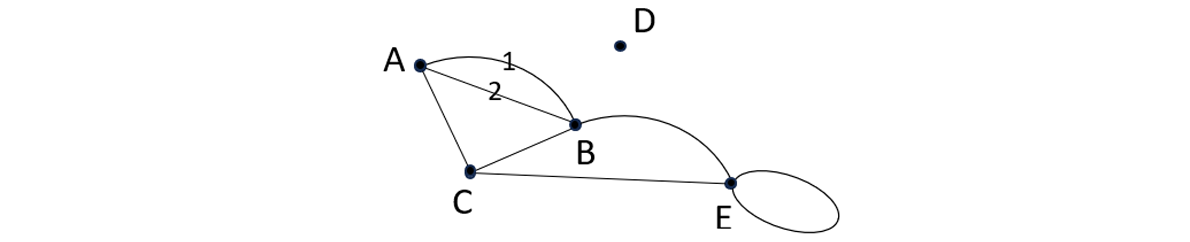
Hình 1 cho ta một Graph có:
Các đỉnh: A, B, C, D, E.
Bậc của các đỉnh: A = 3, B = 4, C = 3, D = 0, E = 4.
Các cạnh: AB, BA, AC, CB, BE, EC.
Khuyên: EE.
Đỉnh cô lập: D.
Các đỉnh kề nhau: A - B, A - C, B - C, C - E, …
Các cạnh liên tiếp: AB – BC, BC – CE, AB – BE, …
Theo định nghĩa thì một
Graph dù có cạnh cong hay thẳng, dài hay gắn, các đỉnh nằm ở vị trí nào không
quan trọng. Điều mà người ta quan tâm là Graph có bao nhiêu đỉnh, bao nhiêu cạnh
và các cạnh được nối với nhau bởi các đỉnh nào. Do đó các hình sau đây đều biểu
thị cho cùng một Graph.
Rõ ràng là một cạnh Graph có 2 đầu mút (kể cả khuyên), đó đó tổng số bậc của tất cả các đỉnh phải bằng 2 lần tổng số cạnh. Và do đó tổng số đỉnh có bậc lẽ của một Graph phải bằng 0, 2, 4, 6, …v..v..
Graph
có liên hệ rất nhiều trong đời sống hàng ngày của con người. Một số ví dụ cụ thể
nhất về Graph là hệ thống giao thông của một thành phố, một quốc gia… hay hệ thống
mạng Internet chẳng hạn. Những hệ thống này đều mô phỏng lại một Graph cụ thể
nào đó.
Giả sử ta có một Graph G và
hai đỉnh A và B của G. (G là bản đồ giao thông của một thành phố chẳng hạn và
A, B là 2 địa điểm nào đó của bản đồ). Chúng ta sẽ quan tâm đến những vấn đề
như có bao nhiêu đường nối từ A đến B, đường nối nào ngắn nhất.
Ta có các khái niệm sau đây:
Một dẫy các cạnh liên tiếp nối A và B được gọi là một đường đi từ A đến B, khi đó A sẽ được gọi là đầu đường và B là cuối đường.
Ví dụ trong hình 1 ta có các lựa trọn về đường đi từ A
đến E như sau.
A1BE; A2BE; ACE; ACBE; A1BCE; A2BCE; A1B2ACE; A1BCA2BE; …
Hai đỉnh được gọi là liên thông với nhau nếu có đường đi nối giữa chúng. Một Graph được gọi là liên thông nếu mọi đỉnh của nó đều liên thông với nhau.
Vẫn trong hình 1 ở trên, ta có các đỉnh A; B; C; E là liên thông với nhau còn đỉnh D không liên thông với đỉnh nào.
Một đường đi khép kín (có đầu đường trùng với cuối đường) được gọi là một chu trình.
Ví dụ chu trình ABECA được mô tả bằng màu đỏ trong hình trên.
Một đường đi (chu trình) gọi là sơ cấp nếu nó không đi qua đỉnh nào 2 lần trở lên.
Một đường đi (chu trình) gọi là đơn giản nếu nó không đi qua cạnh nào 2 lần chở lên.
Định lý 1:
Cho Graph G có tất cả các đỉnh là bậc chẵn khác không. Ta sẽ chứng minh từ bất
kỳ đỉnh nào của G đều có thể vẽ được một chu trình đơn giản.
Thật vậy, từ đỉnh A của G
ta đi theo đường AB rồi từ B lại đi theo BC,… mỗi lần đi ta sẽ đi theo một đường
mới, vì các đỉnh của G đều có bậc chẵn nên mỗi lần đi đến một đỉnh nào đó thì sẽ
có một đường khác từ đỉnh đó để đi ra. Do các đỉnh của G là hữu hạn nên đến một
lúc nào đó ta sẽ đi quay lại đỉnh A và ta có một Chu trình đơn giản.
Ta có các khái niệm khác sau đây.
Một đường đi qua tất cả các cạnh của G mà mỗi cạnh chỉ đi qua một lần gọi là đường đi Euler của G.
Một chu trình đi qua tất cả các cạnh của G mà mỗi cạnh chỉ đi qua một lần gọi là một chu trình Euler của G.
Định lý 2:
Một Graph G có chu trình Euler khi và chỉ khi G liên thông và mọi đỉnh của G đều
có bậc chẵn.
Trước hết ta chứng minh. “G
có chu trình Euler thì G liên thông và mọi đỉnh của G đều có bậc chẵn”.
Thật vậy, theo định nghĩa
của chu trình Euler thì hiển nhiên G liên thông. Giả sử chu trình Euler của G bắt
đầu từ đỉnh A khi đó tất cả các đỉnh mà nó đi qua đều có số lần đi vào và đi ra
là như nhau nên các đỉnh này đều có bậc chẵn. Với đỉnh A thì bắt đầu là đi ra
và kết thúc là đi vào nên A cũng có bậc chẵn.
Bây giờ, “Giả sử G
liên thông và có tất cả các đỉnh là bậc chẵn. Ta chứng minh G có chu trình
Euler”.
Thật vậy, theo định lý 1 ở
trên thì do G có tất cả các đỉnh là bậc chẵn nên từ bất kỳ điểm nào ta cũng vẽ
được một chu trình đơn giản. giả sử từ điểm A ta vẽ được chu trình đơn giản p1 ta
sẽ tô tất cả các cạnh của p1 bằng mầu đỏ, các cạnh còn lại của G sẽ tô mầu trắng
và ta gọi là G’. Do G có tất cả các đỉnh là chẵn nên G’ cũng có tất cả các đỉnh
là chẵn. Vì G liên thông nên giữa G và G’ sẽ có ít nhất một điểm chung giả sử
là điểm B. Lại theo định lý 1, từ B ta vẽ được chu trình p2 của G’ (tô bằng mầu
xanh). Bây giờ ta vẽ lại p1 và p2 thành một chu trình đơn giản theo cách sau. Từ
A đi theo các đường màu đỏ đến B rồi từ B đi theo các đường màu xanh cho đến
khi về lại B, tiếp tục từ B đi theo các đường màu đỏ để về lại A. Ta gọi chu
trình đơn giản này là p1’ (tô bằng màu vàng). Tiếp tục lặp lại quá trình trên để
tìm p2’… cứ như vậy cho đến khi nào tất cả các cạnh mầu trắng đều được tô bằng
màu khác thì ta có một chu trình Euler. (đpcm)
Ta xem minh họa ở video sau
đây:
Ví dụ: Vẽ hình sau bằng
1 nét.
Việc vẽ hình bằng 1 nét bút thực ra là việc tìm một đường đi (hoặc chu trình) Euler dó đó.
Từ định lý ở trên ta dễ dàng có được kết quả sau đây.
Một hình H sẽ vẽ được bằng 1 nét nếu nó có nhiều nhất 2 đỉnh lẽ.
Thật vậy, giả sử 2 đỉnh lẽ
của hình H là A và B, ta sẽ vẽ thêm một đường nối giữa A với B khi đó mọi đỉnh
của hình H đều có bậc là chẵn. Ta vẽ 1 chu trình Euler từ A đi qua tất cả các cạnh
của H đến B rồi kết thúc ở A bằng đường vẽ thêm. Như vậy, nếu ta bỏ đường vẽ
thêm thì ta có 1 đường đi Euler có điểm đầu là A và điểm cuối là B.
Để vẽ hình bằng một nét ta làm như sau.
Nếu Hình không có đỉnh lẽ thì ta có thể bắt đầu vẽ ở bất cứ đỉnh nào.
Nếu hình có 2 đỉnh lẽ thì ta phải bắt đầu vẽ từ một đỉnh lẽ và kết thúc ở một đỉnh lẽ còn lại.
Ta xem lời giải của hình 3a và 3b qua video sau đây:
Đầu tiên Euler đã mô hình
hoá toán học cho câu đó như sau.
Coi các vùng đất của
thành phố là các đỉnh của một Graph, các cây cầu nói 2 vùng đất với nhau là các
cạnh ta sẽ có một Graph sau đây.
Nhìn vào hình
vẽ ta thấy cả 4 đỉnh của Graph đều có bậc lẽ, do đó nó không thể vẽ được bằng một
nét hay không có đường đi Euler. Nói cách khác câu đố này không có lời giải.
Khương Hậu
-----------------------------------------------------
BÀI VIẾT CÙNG CHUYÊN MỤC
Graph Toán học và trò chơi vẽ hình một nét
Định lý Thales và ứng dụng đo đạc
Cách vẽ ngôi sao năm cánh chuẩn bằng thước và compa
------------------------------------------------------
SHOP HIỀN HẬU








Không có nhận xét nào:
Đăng nhận xét